arisaka444のブログ

ツイッター（@arisaka444）

R による酵素反応速度論的解析

　ある酵素反応がミカエリス・メンテンの速度論に従うと仮定し、ミカエリス定数 Km や最大反応速度 Vmax を実験値から推測する事がよく行われます。古典的には、 Lineweaver-Burk plot (LB plot) 等が利用されてきました。しかし LB plot は、基質濃度が低くなるほど誤差が増幅される、Km 値等を算出する際に大きな外挿を要する、といった問題点が指摘されています。そのため LB plot に代わる様々な計算手法が提案されてきました。
　本記事では、Two-parameter Michaelis-Menten model の適用による Km 値及び Vmax 値の推定例を仮想データを用いて示します。
　
　Two-parameter Michaelis-Menten model は下記の通りです。

f\left(x,\left(d,e\right)\right)=\frac{d}{1+\left(e/x\right)}


上式の d を Vmax 、 e を Km 、 x を [S] に置き換えて変形すれば、ミカエリス・メンテン式と等しい事が確認できます。
　解析対象とする仮想データは下記の通りとします。 [S] は基質濃度、V は酵素反応速度 (初速度) です。

f:id:arisaka444:20210619222834p:plain

　以下に与えられた仮想データの分析の一例を示します。drc パッケージの関数を用いて、観測値より上式のパラメータ d 及び e を推定する事で Vmax 、 Km を求めます。

install.packages("drc") #パッケージのインストール（初回のみ）
S <- c(0.2, 0.5, 1.0, 2.0, 3.0)
V <- c(0.015, 0.029, 0.038, 0.044, 0.048)
library(drc)
mm <- drm(V ~ S, fct = MM.2())
summary(mm)

次のような出力が得られます。

Model fitted: Michaelis-Menten (2 parms)

Parameter estimates:

               Estimate Std. Error t-value   p-value    
d:(Intercept) 0.0556745  0.0013655  40.771 3.247e-05 ***
e:(Intercept) 0.4886506  0.0400870  12.190  0.001189 ** 
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error:

 0.001000946 (3 degrees of freedom)

パラメータ d の推定値が 0.0556745 、 e の推定値が 0.4886506 となりました。これらが Vmax 及び Km となります。
　得られたモデルの実験値に対する当てはまりの良さを視覚的に確認してみましょう。

plot(mm, log="", xlab="[S]", ylab="V",xlim=c(0, 4), ylim=c(0,0.06))

f:id:arisaka444:20210314051947p:plain

　Km 、 Vmax 、 (1/2)Vmax を青色の破線で書き加えると、次のようになります。

plot(mm, log="", xlab="[S]", ylab="V",xlim=c(0, 4), ylim=c(0,0.06), )
Vmax <- mm$coefficients[1]
Km <- mm$coefficients[2]
abline(h=Vmax, col="blue",lty=2)
segments(-1, Vmax/2, Km, Vmax/2, col="blue", lty=2)
segments(Km, -1, Km, Vmax/2, col="blue", lty=2)
mtext(text="Km", col="blue", side=1, line=1, at=Km)

f:id:arisaka444:20210619223042p:plain

横軸と平行な青線のうち、上の破線は Vmax 、下の破線は (1/2)Vmax に対応しています。 Km 値を表す縦の破線と (1/2)Vmax の破線が曲線上で交わっている事が確認できます。

　本記事は以上です。何かの参考になれば幸いです。


[参考]
MM: Michaelis-Menten model in drc: Analysis of Dose-Response Curves
RPubs - Fitting a Michaelis-Menten model and drawing the results in R
Ｒで致死試験の用量応答曲線を描く - 環境質リスク管理研究室のブログ

基本情報技術者試験を振り返って

令和元年度秋期基本情報技術者試験を受験しました。受験の理由は、なんとなく情報技術について勉強したくなったからです。結果を先に書くと、ぎりぎり合格でした。

本記事では、基本情報技術者試験の受験の過程を大雑把に振り返ります。そして反省点などを明らかにして、今後に活かしたいと思います。記録の確認はせず、記憶頼りに書いていくので、正確性には欠けているかもしれません。

受験申し込みをしたのは令和元年7月の中頃で、その直後から午前試験の参考書を読み始めました。1ヶ月ほど掛けて少しずつ通読しましたが、全体的な雰囲気はわかったものの、あまり身につきませんでした。

参考書を読み直しても深く理解できる気がしなかったため、午前試験の過去問演習に着手しました。着手直後はあまり勉強時間が確保できず進捗はよくありませんでしたが、8月の末頃は比較的集中して過去問を解くことができました。結果として、午前試験2年分すなわち4回分、また、言語問題とアルゴリズム問題を除く午後試験3回分を解くことができました。このときの過去問演習が最も試験合格に寄与したと思います。午前試験の過去問は以降もときどき解きました。

9月から表計算の参考書を読み始めました。1週間程度で読み終えるつもりでしたが、様々な用事があったため、なかなか勉強時間が確保できず、通読するのに2週間程度掛かりました。参考書がわかりやすく、また、Excelの使用経験があったため、内容は比較的よく理解できました。参考書を読み終えたあとは、過去問を1年分解きました。予定していたより試験の勉強ができなかったため、焦り始めた月でした。

9月末頃からアルゴリズムの参考書に着手しました。試験まで時間があまり残されていないため集中して勉強したかったのですが、10月になってからスケジュールが厳しく、なかなか勉強時間が確保できませんでした。そこで、アルゴリズムの参考書は7割程度読み進めたところですべて読み切ることを諦め、試験日の1週間ほど前からアルゴリズムの過去問を解きました。アルゴリズム以外の分野の過去問も苦手分野を重点的に解き、試験日の直前は徹夜せずに早めに寝て、よい体調で受験できるよう努めました。

よく寝たおかげで試験当日はかなりよい体調でした。このときの体調も、試験合格に大きく寄与していたと思います。また、午前試験は過去問で解いたことのある問題がいくつも見られました。運が良かったのかもしれません。

試験の後、公式解答で自己採点してみたところ、正答割合が午前午後ともに６割5部を超えていたため、おそらく合格しているだろうと思われました。ただし、午後試験は正答割合が6割を超えていても配点によっては不合格になることがあるという噂を聞いていたので、不安が残りました。

試験日の約1ヶ月後、公式サイトで合否の確認をしました。午前午後ともに60点台後半で、試験の合格が明らかになりました。

こうして基本情報技術者試験を振り返ってみると、受験の目標が、情報技術に関する知識の習得から試験の合格に変化してしまったことが少し残念です。勉強時間が想定よりも確保できなかったことが一因だと思われます。情報技術の知識は、あまり身についた気がしません。

今後、資格試験を受験する際は、十分な勉強時間を掛けて、試験合格だけに止まらない知識を身につけたいと思います。

不偏分散の期待値について

偏差平方和を標本の大きさで割って得られる標本分散S ^ { 2 }、および、偏差平方和を自由度で割ることにより得られる不偏分散U ^ { 2 }について、次のように定められる。

S ^ { 2 } = \frac { 1 } { n } \sum _ { i = 1 } ^ { n } \left( X _ { i } - \overline { X } \right) ^ { 2 }

U ^ { 2 } = \frac { 1 } { n - 1 } \sum _ { i = 1 } ^ { n } \left( X _ { i } - \overline { X } \right) ^ { 2 }

不偏分散は母分散の不偏推定量であり、その期待値は母分散に等しい。本記事では、この事実を計算により確認する。


まずは、標本分散S ^ { 2 }の期待値を確認する。

E \left[ S ^ { 2 } \right]

= E \left[ \frac { 1 } { n } \sum _ { i = 1 } ^ { n } \left( X _ { i } - \overline { X } \right) ^ { 2 } \right]

= \frac { 1 } { n } \sum _ { i = 1 } ^ { n } E \left[ \left\{ \left( X _ { i } - \mu \right) - ( \overline { X } - \mu ) \right\} ^ { 2 } \right]

= \frac { 1 } { n } \sum _ { i = 1 } ^ { n } E \left[ \left( X _ { i } - \mu \right) ^ { 2 } - 2 \left( X _ { i } - \mu \right) ( \overline { X } - \mu ) + ( \overline { X } - \mu ) ^ { 2 } \right]

= \frac { 1 } { n } \sum _ { i = 1 } ^ { n } \left( E \left[ \left( X _ { i } - \mu \right) ^ { 2 } \right] - 2 E \left[ \left( X _ { i } - \mu \right) ( \overline { X } - \mu ) \right] + E \left[ ( \overline { X } - \mu ) ^ { 2 } \right] \right)

= \frac { 1 } { n } \sum _ { i = 1 } ^ { n } \left( V [ X ] - 2 E \left[ \left( X _ { i } - \mu \right) ( \overline { X } - \mu ) \right] + V [ \overline { X } ] \right)

= \frac { 1 } { n } \sum _ { i = 1 } ^ { n } \left( \sigma ^ { 2 } - 2 E \left[ \left( X _ { i } - \mu \right) ( \overline { X } - \mu ) \right] + \frac { \sigma ^ { 2 } } { n } \right)

= \sigma ^ { 2 } - \frac { 2 } { n } \sum _ { i = 1 } ^ { n } E \left[ \left( X _ { i } - \mu \right) ( \overline { X } - \mu ) \right] + \frac { \sigma ^ { 2 } } { n }

ここで

\sum _ { i = 1 } ^ { n } E \left[ \left( X _ { i } - \mu \right) ( \overline { X } - \mu ) \right]

= E \left[ ( \overline { X } - \mu ) \sum _ { i = 1 } ^ { n } \left( X _ { i } - \mu \right) \right]

= E \left[ ( \overline { X } - \mu ) \left( \sum _ { i = 1 } ^ { n } X _ { i } - \sum _ { i = 1 } ^ { n } \mu \right) \right]

= E [ ( \overline { X } - \mu ) ( n \overline { X } - n \mu ) ]

= n E [ ( \overline { X } - \mu ) ( \overline { X } - \mu ) ]

= n E \left[ ( \overline { X } - \mu ) ^ { 2 } \right]

= n V [ \overline { X } ]

= n \cdot \frac { \sigma ^ { 2 } } { n }

= \sigma ^ { 2 }

したがって

E \left[ S ^ { 2 } \right]

= \sigma ^ { 2 } - \frac { 2 } { n } \sigma ^ { 2 } + \frac { \sigma ^ { 2 } } { n }

= \left( 1 - \frac { 2 } { n } + \frac { 1 } { n } \right) \sigma ^ { 2 }

= \frac { n - 1 } { n } \sigma ^ { 2 }

ゆえに、標本分散S ^ { 2 }の期待値は、母分散\sigma ^ { 2 }には一致せず、母分散を\frac { n - 1 } { n }倍したものとなる。


次に、ここまでの計算結果を利用して、不偏分散U ^ { 2 }の期待値を確認する。

上記で得られた

E \left[ S ^ { 2 } \right] = \frac { n - 1 } { n } \sigma ^ { 2 }

の両辺に\frac { n } { n - 1 }を掛けると

\frac { n } { n - 1 } E \left[ S ^ { 2 } \right] = \sigma ^ { 2 }

より

E \left[ \frac { n } { n - 1 } S ^ { 2 } \right] = \sigma ^ { 2 }

となる。ここで

\frac { n } { n - 1 } S ^ { 2 }

= \frac { n } { n - 1 } \cdot \frac { 1 } { n } \sum _ { i = 1 } ^ { n } \left( X _ { i } - \overline { X } \right) ^ { 2 }

= \frac { 1 } { n - 1 } \sum _ { i = 1 } ^ { n } \left( X _ { i } - \overline { X } \right) ^ { 2 }

これは、不偏分散U ^ { 2 }にほかならない。

すなわち

E \left[ U ^ { 2 } \right] = \sigma ^ { 2 }

であり、不偏分散の期待値は母分散に等しい。


【参考文献】
回帰分析入門、豊田秀樹 編、東京図書、2012

もしヒトに光合成の能力があったならば

もしわれわれ人間が、光合成のみで生きていくことができるならば、毎日食事をする必要がなくなり、食事をするためのお金を得る必要がなくなり、お金を得るために働く必要すらなくなるかもしれません（食事以外でお金を使うならば別ですが）。そうなれば、日々の労働の苦労から解放されるでしょう。

もちろん、われわれ人間は光合成の能力を持っていません。

しかし、もし人間が光合成を行うことができるとしたら、果たして光合成に依存して生きていくことはできるのでしょうか。

「光合成とはなにか」（園池 公毅、講談社ブルーバックス、2008）という本のコラム（『動物の光合成』）に、上記の疑問に答えてくれる内容が記載されています。

それによると、人間の場合、光合成に依存して生きていくのは難しいようです。というのも、人間の活動に必要なエネルギーを光合成でまかなおうとすると太陽光を受ける面積がかなり必要で、人間の体表面の面積では到底足りないからだそうです。

ただし、世の中には光合成に依存して生きている動物が存在し、同コラムではそういった動物についても取り上げています。

光合成というとまず植物が思い浮かびますが、動物の光合成という観点もおもしろいものだなと思いました。

。

スピアマンの順位相関係数とピアソンの積率相関係数の関係性を R で確認する



スピアマンの順位相関係数は、データを順位に変換した場合のピアソンの積率相関係数に当たることが知られています。本記事では、このことを、統計解析ソフトウェアの R で簡単に確認できることを示します。

次のような7組のデータがあるとします。

(x, y) = (1, 2), (2, 1), (3, 6), (4, 4), (5, 6), (6, 7), (7, 12)

このデータから R を用いてピアソンの積率相関係数とスピアマンの順位相関係数を算出してみましょう。

とりあえず散布図を描いてみましょう。 R コンソールに下記のコマンドをコピペしてみてください。 

x <- 1:7
y <- c(2,1,6,4,6,7,12)
plot(x,y)



すると次のような図が得られます（コピペしても図が現れない場合は「Enter」キーを押してみてください）。

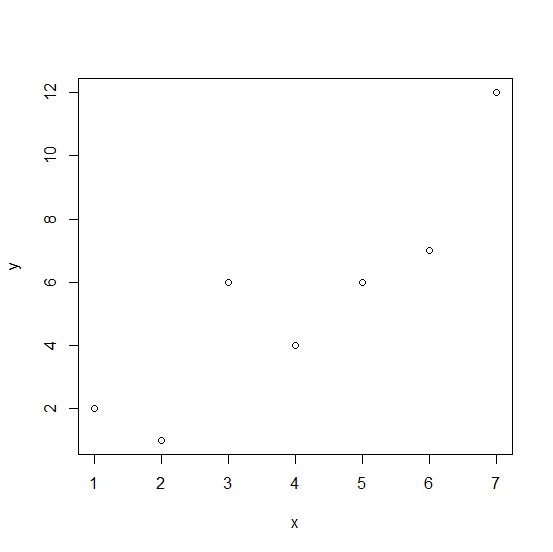
f:id:arisaka444:20190324035026p:plain

ふたつの相関係数は下記のコマンドで算出できます。 

cor(x,y)
cor(x,y,method="spearman")



出力結果は次のようになります。

> cor(x,y)
[1] 0.8890009
> cor(x,y,method="spearman")
[1] 0.9009375

出力結果から、ピアソンの積率相関係数を r 、スピアマンの順位相関係数を ρ とするならば、r = 0.8890009、ρ = 0.9009375 であることがわかります。

次に、rank 関数を用いてデータを順位データに変換した上で、ピアソンの積率相関係数を算出してみましょう。rank 関数は測定値を小さい順に 1, 2, 3,・・・と順位に変換することができます。ただし、タイ(同一の値の組)は平均化されます [1] 。次のコマンドを入力してみてください。 

 cor(rank(x),rank(y))



次のような出力が得られます。 

> cor(rank(x),rank(y))
[1] 0.9009375



順位データに変換した場合のピアソンの積率相関係数は r = 0.9009375 となり、先ほど算出したスピアマンの順位相関係数に一致しましたね。

このように、R の rank 関数を用いると、スピアマンの順位相関係数が、データを順位に変換した場合のピアソンの積率相関係数に一致することが確認できます。

最後に、データをそのまま利用した場合と順位データに変換した場合の散布図をまとめて下記に示します。図中に相関係数も記入しました。

f:id:arisaka444:20190324035132p:plain

[1] ソート、オーダー、ランク - RjpWiki
http://www.okadajp.org/RWiki/?%E3%82%BD%E3%83%BC%E3%83%88%E3%80%81%E3%82%AA%E3%83%BC%E3%83%80%E3%83%BC%E3%80%81%E3%83%A9%E3%83%B3%E3%82%AF

「平均の平均」と「全体の平均」が一致するとき



例を用いて説明します。構成人数20人のグループAと構成人数30人のグループBに算数のテストを受けさせたところ、グループAの平均点は50点、グループBの平均点は60点であったとします。このような場合、グループAとBを合わせた「全体の平均点」は、Aの平均点とBの平均点の相加平均（単純平均、算術平均とも）ではなく、グループごとの人数を重みとした加重平均で求めなければなりません。すなわち

\frac { 50 + 60 } { 2 } = 55

と計算するのは誤りで、

\frac { 50 \times 20 + 60 \times 30 } { 20 + 30 } = 56

が正解です。

ところが、両グループの人数が等しい場合は、平均点と平均点の相加平均と「全体の平均点」（加重平均）が一致します。たとえば前述の例において、両グループの人数がどちらも20人であったならば、両グループの平均点の相加平均は先程と同様に

\frac { 50 + 60 } { 2 } = 55

のままですが、加重平均は

\frac { 50 \times 20 + 60 \times 20 } { 20 + 20 } = 55

となります。このような場合、相加平均で計算しても加重平均で計算しても結果は一致します。

より一般化して考えてみましょう。n個の平均値の相加平均は

\frac { \sum _ { i = 1 } ^ { n } \overline { x } _ { i } } { n }

です。 一方で、n個の平均値の加重平均は

\frac { \sum _ { i = 1 } ^ { n } \overline { x } _ { i } w _ { i } } { \sum _ { i = 1 } ^ { n } w _ { i } }

となります。この式は、もしそれぞれの重みの大きさw _ { i }が等しかった場合は

\frac { \sum _ { i = 1 } ^ { n } \overline { x } _ { i } w } { \sum _ { i = 1 } ^ { n } w }

= \frac { w \sum _ { i = 1 } ^ { n } \overline { x } _ { i } } { n w }

= \frac { \sum _ { i = 1 } ^ { n } \overline { x } _ { i } } { n }

となります。すなわちn個の平均値の相加平均と全く同じ式になります。

このように、重みの大きさがすべて等しい加重平均は相加平均に一致します。このため、前述したテストの例のように「平均の平均」と「全体の平均」が一致する結果が生じます。この知識は、計算量を減らしたい場合などに役立つかもしれません。

ゴルトンボードについて


https://m.youtube.com/watch?v=6YDHBFVIvIs

上記の動画で取り上げられている装置は、ゴルトンボード（Galton Board）と言います。（理想的には）ベルヌーイ試行（確率p=0.5で右、1-p=0.5で左）が繰り返されるので、最終的に球が落ちる位置は二項分布に従います。釘の段数を増やせば分布が正規分布に近づく様子を見て取ることもできます。つまり、試行回数nを増やせば二項分布は正規分布に近づくというド・モアブル–ラプラスの定理（中心極限定理の特別な場合）を視覚的に確認できるのです。

二項分布に従うことをもう少し具体的に書きます。たとえばボードの底に左から順番に0,1,2,・・・と番号をつけたとき、釘に当たるたびに球が左にしか跳ねなければ（右に0回跳ねたなら）球は0番に到達します。途中で1回だけ右に跳ねれば1番です。n回跳ねたうちのk回右に跳ねればk番ですね。これは、二項分布の解説でよく使われる例、コインをn回投げてk回表が出ることと似ていますね。いわば、球が釘に当たるたびに、運命の女神がコインを振り、表が出れば右、裏が出れば左と決めているようなものであります。

f:id:arisaka444:20181216012805j:plain f:id:arisaka444:20181216012920j:plain

3段の場合を例に図で表してみました（上図）。 左にしか跳ねなければ0番に到達し、途中で1回だけ右に跳ねれば1番に到達しています。この図の場合、k番に到達する確率は、試行回数n=3、生起確率p=0.5の二項分布B(3 , 0.5)ですから P ( X = k ) = _ { 3 } C _ { k } 0.5 ^ { k } ( 1 - 0.5 ) ^ { 3 - k } で求められます（たとえばk = 2のとき0.375）。

f:id:arisaka444:20181216012955j:plain f:id:arisaka444:20181216013012j:plain

なお、パスカルの三角形を重ねると、k番に到達する経路の数がわかります。上の２つの図は3段のゴルトンボードと4段のパスカルの三角形です。 この2つの図を重ねると、たとえば1番に到達する経路が3つ存在することがわかります。もちろん、順列や組合せを利用しても経路の数はわかります。

釘を三角形状に並べてゴルトンボードを作製する場合、必要になる釘の本数は何本になるでしょうか。ゴルトンボードの段数が1段、2段、3段、・・・と増すにつれて、必要な釘の本数は1本、1+2本、1+2+3本、・・・と増加していきます。したがって、n段のゴルトンボードを作製するのに必要な釘の本数は、初項1、公差1、項数nの等差数列の和で表せます。すなわち、

\sum _ { i = 1 } ^ { n } i = \frac { n ( n + 1 ) } { 2 }

となります。上式から、たとえば、10段のゴルトンボードであれば必要な釘の本数は55本、50段であれば1275本、100段であれば5050本であることがわかります。段数を増やすほど分布は正規分布に近づきますが、一方で作製に必要な釘の本数は二次関数的に増加し、作製に必要な労力も巨大になってゆくということです（なお、三角形状以外の形状のゴルトンボードも存在します）。

以上の記事は、ゴルトンボードに関する英語のウェブサイトを参考にして書きました。より詳細で正確な情報を得たい方は英語の解説記事を調べることをおすすめします。また、この記事に書いた内容はあくまで理想上のもので、おそらく実物を作製する際は細かい調整が必要になると思われます。最後に、本記事の内容に間違っている点などがございましたら、コメントで教えていただけると助かります。

更新情報 : 2019.4.1 作製に必要な釘の本数について追記